【特惠】26考研
红包
【考研】专业课HOT
26考研
【MBA】在职考研
【5月】高分训练营
【报录比】查询
计划
【真题】历年考题
资料
【申硕】同等学力
预备
【词汇】5500大纲
免费
【在线】英语测评
免费
【资料】考研大纲
精

扫码加入训练营
牢记核心词
学习得礼盒
2022考研数学新大纲变化详细解析
2022考研数学一大纲如约而至,对考生而言,最 重要的,最 关心的莫过于考研大纲变动部分,以下,针对考研数学一,新东方在线考研小编对考研大纲变动部分作以说明。
2022考研大纲已于今日9月14日公布,新东方在线考研2022考研大纲直播解析正在进行中!2022考研数学大纲解析已出炉!快一起来看看吧。



添加班主任领资料
添加考研班主任
免费领取考研历年真题等复习干货资料

 推荐阅读
推荐阅读
2024考研数学三大纲变化大不大?变动解析!!考研大纲是中国硕士研究生入学考试的重要指导文件,它详细列出了各科目的考试范围和内容。
来源 : 网络 2023-09-22 08:35:00 关键字 : 2024考研数学三大纲变化
2024考研数学三大纲下载电子版!考研大纲是中国硕士研究生入学考试的重要指导文件,它详细列出了各科目的考试范围和内容。包括公共课(政
来源 : 网络 2023-09-22 08:35:00 关键字 : 2024考研数学三大纲下载
2024考研数学三大纲解析电子版PDF!考研大纲是中国硕士研究生入学考试的重要指导文件,它详细列出了各科目的考试范围和内容。包括公共课
来源 : 网络 2023-09-22 08:35:00 关键字 : 2024考研数学三大纲解析
2024考研数学三大纲原文及变动解析!考研大纲是中国硕士研究生入学考试的重要指导文件,它详细列出了各科目的考试范围和内容。包括公共
来源 : 网络 2023-09-22 08:35:00 关键字 : 2024考研数学三大纲原文
2024考研数学二大纲变化大不大?变动解析!!考研大纲是中国硕士研究生入学考试的重要指导文件,它详细列出了各科目的考试范围和内容。
来源 : 网络 2023-09-22 08:35:00 关键字 : 2024考研数学二大纲变化

 资料下载
资料下载
扫码添加【考研班主任】
即可领取资料包
扫码添加【考研班主任】
即可领取资料包
扫码添加【考研班主任】
即可领取资料包
扫码添加【考研班主任】
即可领取资料包
扫码添加【考研班主任】
即可领取资料包
扫码添加【考研班主任】
即可领取资料包
新东方在线考研资料合集
下载方式:微信扫码,获取网盘链接

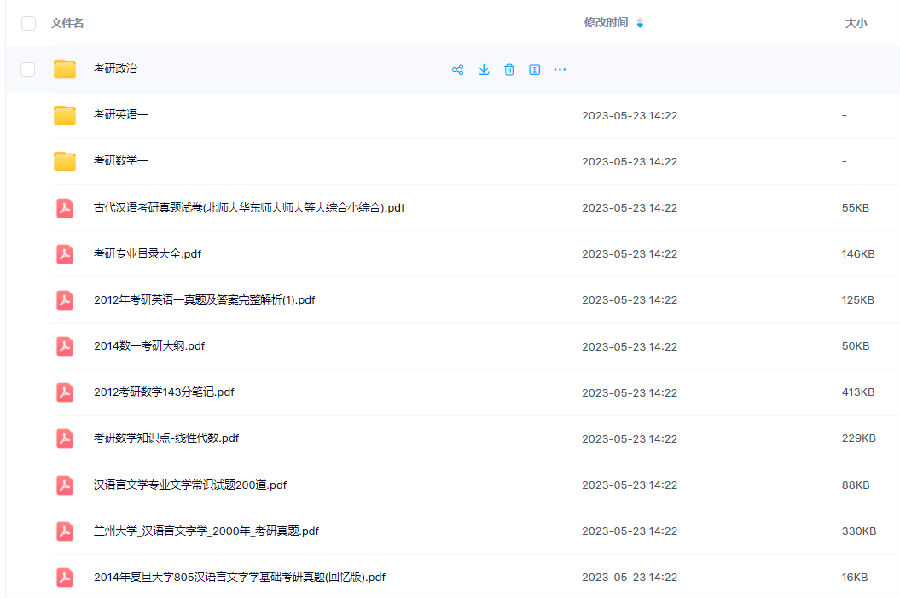
目录:
1.2013-2023年近10年政数英真题及解析PDF版(新东方)
2.2013-2023年专业课考试历年真题及解析PDF版
3.24考研复习备考资料大合集:大纲+备考资料+词汇书+考前押题+自命题
资料介绍:
1.2013-2023年近10年政数英真题及解析PDF版(新东方)
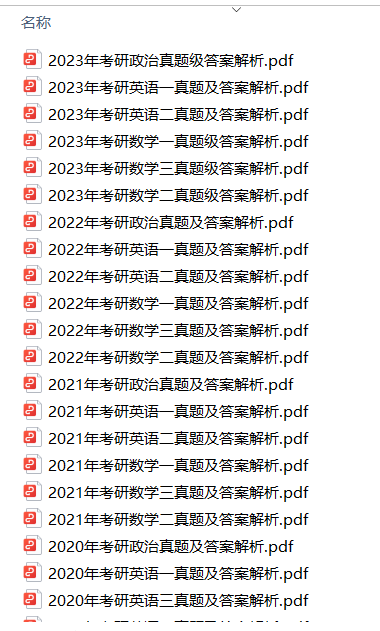 、
、
2.2013-2023年专业课考试历年真题及解析PDF版


3.24考研复习备考资料大合集
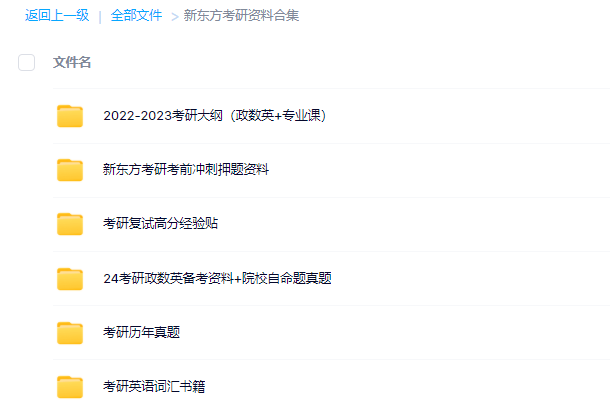
3.24考研复习备考资料:考研大纲
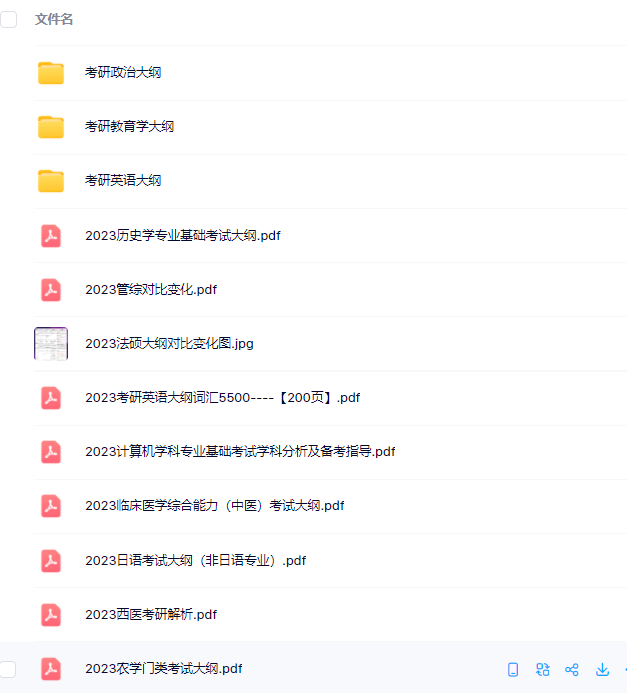
3.24考研复习备考资料:政数英备考资料+自命题真题
------------------
考研备考过程中,尤其是专业课部分,参考往年的考试真题,对于我们的复习有更好的帮助。北京大学考研真题资料都有哪些?小编为大家进行了汇总。
北京大学考研真题资料-公共课
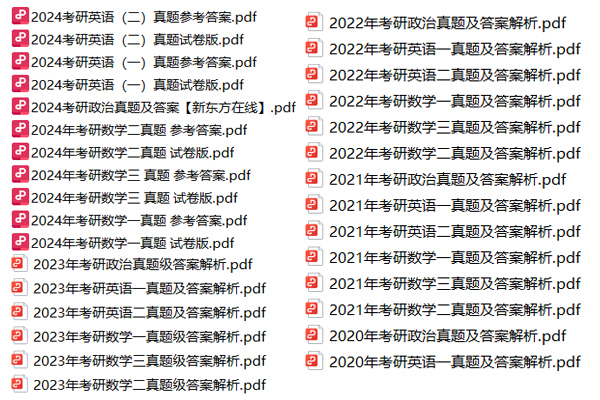
北京大学考研真题资料-专业课


以上就是关于“北京大学考研真题资料下载(历年汇总)”的整理,更多考研资料下载,请关注微信获取下载地址。
扫码添加【考研班主任】
即可领取资料包
扫码添加【考研班主任】
即可领取资料包
扫码添加【考研班主任】
即可领取资料包
扫码添加【考研班主任】
即可领取资料包
扫码添加【考研班主任】
即可领取资料包
扫码添加【考研班主任】
即可领取资料包
扫码添加【考研班主任】
即可领取资料包
扫码添加【考研班主任】
即可领取资料包
扫码添加【考研班主任】
即可领取资料包
扫码添加【考研班主任】
即可领取资料包
扫码添加【考研班主任】
即可领取资料包
扫码添加【考研班主任】
即可领取资料包
扫码添加【考研班主任】
即可领取资料包
扫码添加【考研班主任】
即可领取资料包
扫码添加【考研班主任】
即可领取资料包
扫码添加【考研班主任】
即可领取资料包
扫码添加【考研班主任】
即可领取资料包
扫码添加【考研班主任】
即可领取资料包
扫码添加【考研班主任】
即可领取资料包
扫码添加【考研班主任】
即可领取资料包
扫码添加【考研班主任】
即可领取资料包
扫码添加【考研班主任】
即可领取资料包
扫码添加【考研班主任】
即可领取资料包

 阅读排行榜
阅读排行榜
 相关内容
相关内容