特惠-26考研冲刺
特惠-27考研课
双证-在职硕士
免联考-同等学力
复试分数线
26复试全面指导
模拟复试面试
26考研-全套真题
26考研估分
保研-路线图
27考研-智能择校
27考研-英语测评
27考研-新大纲对比
热门-计算机择校

扫码加入训练营
牢记核心词
学习得礼盒
考研心理学复习备考过程中,具体的备考指导,对于大家的备考来说有更好地指导意义。具体的考研心理学部分如何备考?需要掌握哪些知识点?为了让参加考研心理学考试的同学,更高效的复习备考。下面小编为大家整理了“考研心理学考点背诵:多元统计分析初步”让我们一起来看看吧!
考研心理学考点背诵:多元统计分析初步
多元线性回归分析
1. 现实生活中,大多数影响因变量的因素不是一个而是多个。在线性回归分析中,如果对2个或2个以上的自变量对因变量影响的现象进行分析,就是多元线性回归分析。 2. 优点:更加接近现实,增强对因变量分析估计的准确性。 3. 缺点:计算复杂、多重共线性。 4. 统计前提: (1)同一元线性回归:线性、正态性、独立性、误差等分散性。 (2)特有的前提:样本容量(被试数:自变量数,被试总数)、自变量的选择、多重共线性。 5. 一般形式:Y = b1X1 + b2X2 + … + bkXk + a bk:偏回归系数;a:常数项 6. 标准化形式:ZY = β1ZX1 + β2ZX2 + … + βkZXk βk:标准回归系数( -1≤βk≤1) 7. 计算:涉及矩阵运算,一般采用专门的计算机软件计算(Excel、SPSS、SAS等)。
多元线性回归方程的检验
1. 对整个方程的检验:F检验 (1)SST:总和方,即Y的和方, dfT = n – 1(被试数 - 1) (2)SSR:线性回归部分的和方,dfR = k(自变量个数), (3)MSR = SSR / dfR (4)SSE = SST - SSR ,残差的和方,dfE = n – 1 – k, (5)MSE = SSE / dfE (6)F = MSR / MSE,F(dfR,dfE) 2. 方程的解释能力: (1)测定系数:R2,回归部分和方占总和方的比例, 0 ≤ R2 ≤ 1 (2)调整后的测定系数:Radj2公式 当k接近于n时,Radj2比R2小很多 当n远大于k时,Radj2 ≈R2 (3)对偏回归系数的检验:t检验 Y = b1X1 + b2X2 + … + bkXk + a ti = (bi – 0) / (SEb) 3. 与一元线性回归不同:某个(或某几个)偏回归系数不显著时,整个回归方程仍有可能是显著的,即F检验显著时,某个(或某几个)t检验可能不显著。 4. 自变量的选择 5. 最优回归方程:整个方程显著且每个偏回归系数显著 6. 最优方程选择法: (1)同时分析法/标准回归(Enter) (2)逐步分析法:顺向进入法/向前回归(Forward)、反向淘汰法/向后回归(Backward) (3)逐步回归法(Stepwise) (4)阶层分析法/分层回归 7. 多重共线性: (1)定义:自变量之间存在较高相关性 (2)问题:大量偏回归系数不显著,标准误增加, I类错误几率增加,偏回归系数不可靠,歪曲研究结果 (3)检验:容限度(tolerance):1 – Ri2;方差膨胀因素(VIF):容限度的倒数,注意VIF>5的情况; (4)解决方法:增加样本容量、删除不必要的自变量(逐步回归、利用已知信息) 、岭回归 、主成分分析、因素分析。
主成分分析
在研究实际问题时,往往需要收集多个变量。但这样会使多个变量间存在较强的相关关系,即这些变量间存在较多的信息重复,直接利用它们进行分析,不但模型复杂,还会因为变量间存在多重共线性而引起较大的误差。 为能够充分利用数据,通常希望用较少的新变量代替原来较多的旧变量,同时要求这些新变量尽可能反映原变量的信息。 主成分分析和因素分析正是解决这类问题的有效方法。它们能够提取信息,使变量简化降维,从而使问题更加简单直观。 1. 主成分分析:考察多个变量间相关性一种多元统计方法。 2. 基本原理:研究如何通过少数几个主成分(principal component)来解释多个变量间的内部结构。即从原始变量中导出少数几个主分量,使它们尽可能多地保留原始变量的信息,且彼此间互不相关。 3. 目的:数据的压缩;数据的解释。 4. 主成分分析基本思想:主成分分析是设法将原来众多具有一定相关性的变量,重新组合成一组新的、互相无关的综合指标来代替原来的指标。 5. 数学上的处理:将原来P个指标作线性组合,作为新的综合指标。 6. 主成分分析数学表达: (1)主成分分析数学表达:设p个原始变量为 x1, x2, … , xp,新的变量(即主成分)为y1, y2, … , yp ,主成分和原始变量之间的关系表示 (2)主成分分析数学表达公式 7. 主成分分析做法: (1)就是用y1(选取的第一个线性组合)的方差来表达,即y1方差越大,表示y1包含的信息越多。因此在所有的线性组合中选取的y1应该是方差最大的,故称y1为第一主成分。 (2)如果第一主成分不足以代表原来P个指标的信息,再考虑选取y2即选第二个线性组合,为了有效地反映原来信息,y1已有的信息就不需要再出现再y2中,称y2为第二主成分。 (3)依此类推可以构造出第三、第四,……,第P个主成分。 8. 主成分分析图解 9. 主成分的选择: (1)被选的主成分所代表的主轴的长度之和占了主轴总程度之和的大部分。 (2)在统计上,主成分所代表的原始变量的信息用其方差来表示。因此,所选择的第一个主成分是所有主成分中的方差最大者。 (3)如果第一个主成分不足以代表原来的个变量,在考虑选择第二个主成分,依次类推。 (4)这些主成分互不相关,且方差递减。 (5)一般要求所选主成分的方差总和占全部方差的80%以上就可以了。当然,这只是一个大体标准,具体选择几个要看实际情况。 (6)如果原来的变量之间的相关程度高,降维的效果就会好一些,所选的主成分就会少一些,如果原来的变量之间本身就不怎么相关,降维的效果自然就不好。 (7)不相关的变量就只能自己代表自己。 10. 计算步骤: (1)对原来的p个变量进行标准化,以消除变量在水平和量纲上的影响。 (2)根据标准化后的数据矩阵求出相关系数矩阵。 (3)求出协方差矩阵的特征根和特征向量。 (4)确定主成分,并对各主成分所包含的信息给予适当的解释(即主成分命名)
因素分析
1. 又称因子分析,与主成分分析类似,它们都是要找出少数几个新的变量来代替原始变量。 2. 因素分析的主要目的是用来描述隐藏在一组测量到的变量中的一些更基本的,但又无法直接测量到的潜变量 (latent variable, latent factor)。 3. 从显性的变量中得到因素: (1)探索性因素分析(EFA):不事先假定因素与变量之间的关系,而让数据“自己说话”。主成分分析是其中的典型方法。 (2)验证性因素分析(CFA):假定因素与变量的关系是部分知道的,即哪个变量对应于哪个因素,虽然尚且不知道具体的系数。 4. 因素分析的数学表达 (1)原始的p个变量表达为k个因素的线性组合变量。 设p个原始变量为x1, x2, ... , xp,要寻找的k个因素(k < p)为f1, f2, ... , fk,因素和原始变量之间的关系 (2)因素分析的数学表达公式 5. 因素分析的相关概念: (1)共同度(Communality):变量xi的信息能够被k个公因素解释的程度,用k个公因素对第i个变量xi的方差贡献率表示,一般要求大于等于0.3。 (2)方差贡献率:第j个公因素对变量xi的提供的方差总和,反映第j个公因素的相对重要程度。 6. 因素分析的计算前提: (1)因素分析要求样本的个数要足够多(样本数至少是变量的5倍以上,同时样本总数在100以上)。 (2)用于因素分析的变量必须是相关的(计算各变量之间的相关矩阵,若大部分相关系数小于0.3,则不适合作因素分析)。 (3)使用Kaiser-Meyer-Olkin检验(简称KMO检验)和 Bartlett球度检验(Bartlett’s test of sphericity)来判断。 (4)KMO检验:KMO统计量在0.7以上时,因素分析效果较好;KMO统计量在0.5以下时,因素分析效果很差。 (5)Bartlett球度检验:显著,p < 0.05。 7. 因素提取的方法: (1)主成分法(Principal components):多数情况下可以使用该方法。通过主成分分析的思想提取公因素,它假设变量是因素的线性组合。 (2)不加权最小平方法(Unweight Least Square):该方法使实际的相关矩阵和再生的相关矩阵之差的平方和达到最小。 (3)加权最小平方法(Generalized Least Square):用变量值进行加权,该方法也是使实际的相关矩阵和再生的相关矩阵之差的平方和达到最小。 (4)最大似然法(Maximum Likelihood):该方法不要求数据服从正态分布,在样本量较大时使用较好。 (5)主轴因素法(Principal Axis Factoring):该方法从原始变量的相关性出发,使得变量间的相关程度尽可能地被公因素解释。 8. 因素数量的确定: (1)用公因素方差贡献率提取:与主成分分析类似,一般累计方差贡献率达到80%以上的前几个因素可以作为最后的公因素。 (2)用特征根提取:一般要求因素对应的特征根要大于1,因为特征根小于1说明该共因素的解释力度太弱,还不如使用原始变量的解释力度大。 (3)根据碎石图选择。 (4)根据可解释度选择。 9. 因素旋转: (1)目的:使因素的含义更加清楚,以便于对因素的命名和解释。 (2)方法:正交旋转、斜交旋转。 (3)方差最大正交旋转(Varimax):最常用的旋转方法。使各因素保持正交状态,但尽量使各因素的方法达到最大,即相对的载荷平方和达到最大,从而方便对因素的解释。 (4)四次方最大正交旋转(Quartimax):该方法倾向于减少和每个变量有关的因素数,从而简化对原变量的解释。 (5)平方最大正交旋转(Equamax):该方法介于方差最大正交旋转和四次方最大正交旋转之间。 (6)斜交旋转(Direct Oblimin):该方法需要事先指定一个因素映像的自相关范围。 (7)Promax:该方法在方差最大正交旋转的基础上进行斜交旋转。 10. 因素命名:一个因素包含了多个原始变量的信息,它究竟反映了原始变量的哪些共同信息?因素分析得到的因素的含义是模糊的,需要重新命名,以便对研究的问题作出合理解释。 可通过考察观察因素载荷矩阵并结合实际问题完成。命名已经不是统计问题,需要更多的实践经验。 11. 计算因素得分: (1)因素得分(factor score)是每个因素在每个样本上的具体取值,它由下列因素得分函数给出 (2)因素得分公式 12. R型因素分析和Q型因素分析: (1)上述从变量群中提取公共因素的方法,又称R型因素分析和R型主成分分析。如果研究个案群的公共因素,则称Q型因素分析和Q型主成分分析。这时只须把调查的n个被试,当作n个变量,其分析方法与R型因素分析完全相同。 13. EFA和CFA: (1)探索的因素分析局限性: 假定所有的因素 (旋转后) 都会影响变量。在实 际研究中,我们往往会假定一个因素之间没有因果关系,所以可能不会影响另外一个因素的变量。 假定变量残差之间是相互独立。实际上,变量的残差之间可以因为单一方法偏差、子因素等因素而相关。 强制所有因素为独立。这虽然是求解因素个数时不得不采用的机宜之计,却与大部分的研究模型不符。最明显的是,自变量与应变量之间是应该相关的,而不是独立的。 这些局限性就要求有一种更加灵活的建模方法,使研究者不但可以更细致地描述变量与因素之间的关系,而且并对这个关系直接 进行测试。而在探索性因素分析中,一个被测试的模型 (比如正交的因素) 往往不是研究者理论中的确切的模型。 验证性因素分析的强项正是在于它允许研究者明确描述一个理论模型中的细节。 因为测量误差的存在,研究者需要使用多个变量。 当使用多个变量之后,我们就有变量的“质量”问题,即有效性检验。 有效性检验就是要看一个变量是否与其所设计的因素有显著的载荷,并与其不相干的因素没有显著的载荷。 可能进一步检验一个变量工具中是否存在单一方法偏 差,一些变量之间是否存在“子因素”。这些测试都要求研究者明确描述变量、因素、残差之间的关系。对这种关系的描述又叫测度模型 (measurement model)。对测度模型的质量检验 是假设检验之前的必要步骤。 验证性因素分析往往用极大似然估计法求解。它往往与结构方程的方法连用。 14. 主成分分析与因素分析的不同: (1)主成分分析中的主成分个数与原始变量个数是一样的,即有几个变量就有几个主成分,只不过最后我们确定了少数几个主成分而已。而因素分析则需要事先确定要找几个成分,也称为因素(factor),然后将原始变量综合为少数的几个因素,以再现原始变量与因素之间的关系,一般来说,因素的个数会远远少于原始变量的个数。 (2)因素分析可以看作是主成分分析的推广和扩展,但它对问题的研究更深入、更细致一些。实际上,主成分分析可以看作是因素分析的一个特例。因素分析在实际中被广泛应用,而主成分分析通常只作为大型统计分析的中间步骤,几乎不再单独使用。 (3)因变量和因素个数的不一致,使得不仅在数学模型上,而且在实际求解过程中,因素分析和主成分分析都有着一定的区别,计算上因素分析更为复杂。 在对主成分和原始变量之间的关系进行描述时,如果主成分的直观意义比较模糊不易解释,主成分分析没有更好的改进方法;因素分析则额外提供了因素旋转(factor rotation) 这样一个步骤,可以使分析结果尽可能达到易于解释且更为合理的目的。 15. 其它说明: (1)主成分分析和因素分析都是多元分析中处理降维的两种统计方法,只有当原始数据中的变量之间具有较强的相关关系时,降维的效果才会明显,否则不适合进行主成分分析和因素分析。 (2)主成分和因素的选择标准应结合具体问题而定。在某种程度上取决于研究者的知识和经验,而不是方法本身。 (3)即使得到了满意的主成分或因素,在运用它们对实际问题进行评价、排序等分析时,仍然要保持谨慎,因为主成分和因素毕竟是高度抽象的量,无论如何,它们的含义都不如原始变量清晰。
以上就是新东方在线考研频道为大家整理的“考研心理学考点背诵:多元统计分析初步”相关内容,希望可以帮助大家,更多考研心理学复习指导内容尽在新东方在线考研频道!
【心理学】资料这里有↑↑↑
本文关键字: 考研经济学资料

 资料下载
资料下载
2014年-2025年考研历年真题汇总
发布时间:2024-04-25扫码添加【考研班主任】
即可领取资料包
考研大纲PDF电子版下载-历年(附解析)
发布时间:2024-04-25扫码添加【考研班主任】
即可领取资料包
2026年考研政数英备考资料zip压缩包
发布时间:2024-04-25扫码添加【考研班主任】
即可领取资料包
考研英语大纲词汇5500打印版(基础必备)
发布时间:2024-04-25扫码添加【考研班主任】
即可领取资料包
新东方在线考试模拟题【12套】
发布时间:2024-04-25扫码添加【考研班主任】
即可领取资料包
2026年考研专业课知识点总结
发布时间:2024-04-25扫码添加【考研班主任】
即可领取资料包
新东方考研资料下载地址
发布时间:2023-05-17新东方在线考研资料合集
下载方式:微信扫码,获取网盘链接

目录:
1.2013-2023年近10年政数英真题及解析PDF版(新东方)
2.2013-2023年专业课考试历年真题及解析PDF版
3.24考研复习备考资料大合集:大纲+备考资料+词汇书+考前押题+自命题
资料介绍:
1.2013-2023年近10年政数英真题及解析PDF版(新东方)
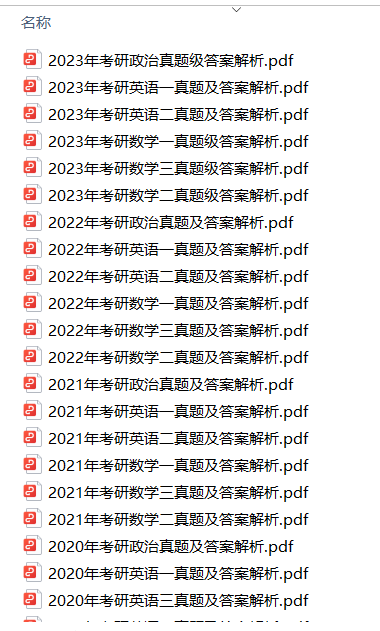 、
、
2.2013-2023年专业课考试历年真题及解析PDF版


3.24考研复习备考资料大合集
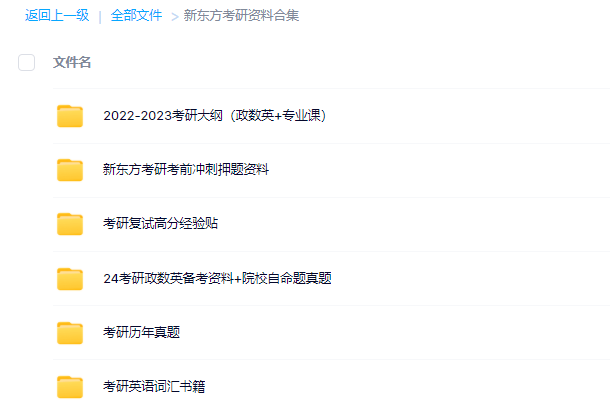
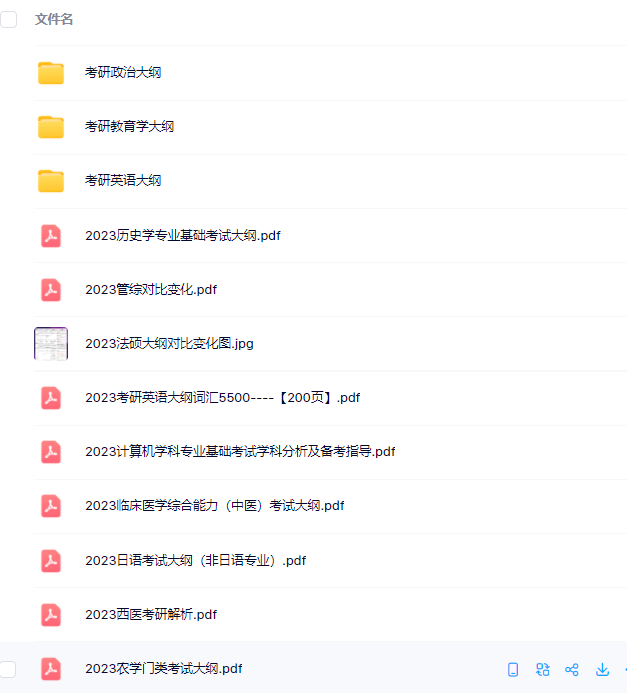
3.24考研复习备考资料:考研大纲
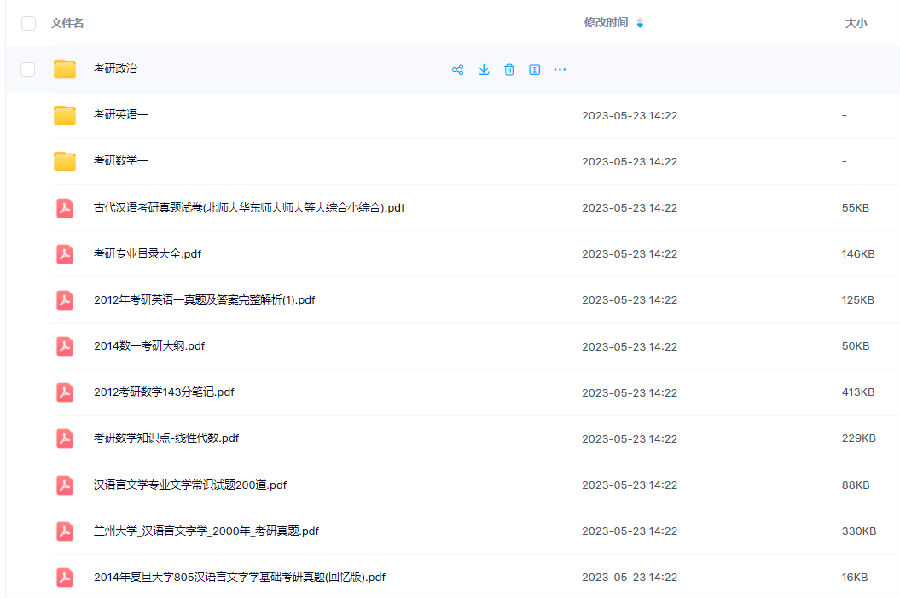
3.24考研复习备考资料:政数英备考资料+自命题真题
------------------
考研备考过程中,尤其是专业课部分,参考往年的考试真题,对于我们的复习有更好的帮助。北京大学考研真题资料都有哪些?小编为大家进行了汇总。
北京大学考研真题资料-公共课
北京大学考研真题资料-专业课


以上就是关于“北京大学考研真题资料下载(历年汇总)”的整理,更多考研资料下载,请关注微信获取下载地址。
2024考研公共课必背知识点汇总
发布时间:2023-01-03扫码添加【考研班主任】
即可领取资料包
2013-2023考研历年真题汇总
发布时间:2023-01-03扫码添加【考研班主任】
即可领取资料包
考研英语大纲词汇(PDF可打印)
发布时间:2023-01-03扫码添加【考研班主任】
即可领取资料包
2024考研专业课知识点总结
发布时间:2023-01-03扫码添加【考研班主任】
即可领取资料包
2023考研政治 内部押题 PDF
发布时间:2022-11-16扫码添加【考研班主任】
即可领取资料包
徐涛:23考研预测六套卷
发布时间:2022-11-16扫码添加【考研班主任】
即可领取资料包
考研政数英冲刺资料最新整理
发布时间:2022-11-16扫码添加【考研班主任】
即可领取资料包
23考研答题卡模板打印版
发布时间:2022-11-16扫码添加【考研班主任】
即可领取资料包
2023考研大纲词汇5500PDF电子版
发布时间:2022-07-28扫码添加【考研班主任】
即可领取资料包
考研历年真题(公共课+专业课)
发布时间:2022-07-28扫码添加【考研班主任】
即可领取资料包
考研英语阅读100篇附解析及答案
发布时间:2022-01-07扫码添加【考研班主任】
即可领取资料包
新东方考研学霸笔记整理(打印版)
发布时间:2022-01-07扫码添加【考研班主任】
即可领取资料包
2001-2021年考研英语真题答案(可打印版)
发布时间:2022-01-07扫码添加【考研班主任】
即可领取资料包
考研英语词汇5500(完整版下载)
发布时间:2022-01-07扫码添加【考研班主任】
即可领取资料包
2022考研政审表模板精选10套
发布时间:2022-01-07扫码添加【考研班主任】
即可领取资料包
历年考研真题及答案 下载
发布时间:2021-12-09扫码添加【考研班主任】
即可领取资料包
考研政审表模板汇总
发布时间:2020-06-17扫码添加【考研班主任】
即可领取资料包
近5年考研英语真题汇总
发布时间:2020-06-17扫码添加【考研班主任】
即可领取资料包
考研英语大纲词汇5500
发布时间:2020-06-17扫码添加【考研班主任】
即可领取资料包
2022考研12大学科专业排名汇总
发布时间:2019-11-21扫码添加【考研班主任】
即可领取资料包
2023考研政治复习备考资料【珍藏版】
发布时间:2019-11-21扫码添加【考研班主任】
即可领取资料包
考研英语万能模板+必备词汇+范文
发布时间:2019-11-21扫码添加【考研班主任】
即可领取资料包
考研数学一、二、三历年真题整理
发布时间:2019-11-21扫码添加【考研班主任】
即可领取资料包

添加班主任领资料
添加考研班主任
免费领取考研历年真题等复习干货资料

 推荐阅读
推荐阅读
2025年(040200)心理学考研考312心理学专业基础的院校名单汇总
来源 : 新东方在线 2024-11-14 11:22:49 关键字 : 心理学考研考312的院校
您在计划中国人民大学心理学考研报考吗?同时也在准备中国人民大学心理学考研辅导和复习吧。首先为您介绍下心理学的研究方向
来源 : 新东方在线 2024-11-27 14:06:06 关键字 : 中国人民大学心理学考研辅导
您在计划北京林业大学心理学考研报考吗?同时也在准备北京林业大学心理学考研辅导和复习吧。首先为您介绍下心理学的研究方向
来源 : 新东方在线 2024-11-15 11:51:06 关键字 : 北京林业大学心理学考研辅导
您在计划北京师范大学心理学考研报考吗?同时也在准备北京师范大学心理学考研辅导和复习吧。首先为您介绍下心理学的研究方向
来源 : 新东方在线 2024-11-15 10:26:06 关键字 : 北京师范大学心理学考研辅导
您在计划首都师范大学心理学考研报考吗?同时也在准备首都师范大学心理学考研辅导和复习吧。首先为您介绍下心理学的研究方向
来源 : 新东方在线 2024-11-18 18:01:06 关键字 : 首都师范大学心理学考研辅导

 资料下载
资料下载
扫码添加【考研班主任】
即可领取资料包
扫码添加【考研班主任】
即可领取资料包
扫码添加【考研班主任】
即可领取资料包
扫码添加【考研班主任】
即可领取资料包
扫码添加【考研班主任】
即可领取资料包
扫码添加【考研班主任】
即可领取资料包
新东方在线考研资料合集
下载方式:微信扫码,获取网盘链接

目录:
1.2013-2023年近10年政数英真题及解析PDF版(新东方)
2.2013-2023年专业课考试历年真题及解析PDF版
3.24考研复习备考资料大合集:大纲+备考资料+词汇书+考前押题+自命题
资料介绍:
1.2013-2023年近10年政数英真题及解析PDF版(新东方)
 、
、
2.2013-2023年专业课考试历年真题及解析PDF版


3.24考研复习备考资料大合集

3.24考研复习备考资料:考研大纲

3.24考研复习备考资料:政数英备考资料+自命题真题

------------------
考研备考过程中,尤其是专业课部分,参考往年的考试真题,对于我们的复习有更好的帮助。北京大学考研真题资料都有哪些?小编为大家进行了汇总。
北京大学考研真题资料-公共课

北京大学考研真题资料-专业课


以上就是关于“北京大学考研真题资料下载(历年汇总)”的整理,更多考研资料下载,请关注微信获取下载地址。
扫码添加【考研班主任】
即可领取资料包
扫码添加【考研班主任】
即可领取资料包
扫码添加【考研班主任】
即可领取资料包
扫码添加【考研班主任】
即可领取资料包
扫码添加【考研班主任】
即可领取资料包
扫码添加【考研班主任】
即可领取资料包
扫码添加【考研班主任】
即可领取资料包
扫码添加【考研班主任】
即可领取资料包
扫码添加【考研班主任】
即可领取资料包
扫码添加【考研班主任】
即可领取资料包
扫码添加【考研班主任】
即可领取资料包
扫码添加【考研班主任】
即可领取资料包
扫码添加【考研班主任】
即可领取资料包
扫码添加【考研班主任】
即可领取资料包
扫码添加【考研班主任】
即可领取资料包
扫码添加【考研班主任】
即可领取资料包
扫码添加【考研班主任】
即可领取资料包
扫码添加【考研班主任】
即可领取资料包
扫码添加【考研班主任】
即可领取资料包
扫码添加【考研班主任】
即可领取资料包
扫码添加【考研班主任】
即可领取资料包
扫码添加【考研班主任】
即可领取资料包
扫码添加【考研班主任】
即可领取资料包

 阅读排行榜
阅读排行榜
 相关内容
相关内容